Στο διαδραστικό σχήμα που μπορείτε να ανοίξετε πατώντας εδώ σας δίνεται η δυνατότητα να διαπιστώσετε μεταξύ άλλων, τη βασική ιδιότητα των σημείων μιας έλλειψης με εξίσωση
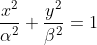
τις διάφορες τιμές της εκκεντρότητας μεταβάλοντας τις τιμές των παραμέτρων α και β καθώς και τις διάφορες θέσεις των εστιών. Ιδαίτερο ενδιαφέρον παρουσιάζει η περίπτωση όπου η έλλειψη "εκφυλίζεται" σε κύκλο.
τις διάφορες τιμές της εκκεντρότητας μεταβάλοντας τις τιμές των παραμέτρων α και β καθώς και τις διάφορες θέσεις των εστιών. Ιδαίτερο ενδιαφέρον παρουσιάζει η περίπτωση όπου η έλλειψη "εκφυλίζεται" σε κύκλο.